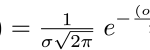Probability

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
And the key problem that the Euclidean distance measure fails to account for is the variability in the data.
Let's go back to our examples.
Here's this sort of work sound this approximate at the beginning of the word one, and here's the worst sound here.
We're going to measure the distance between those two things, and then we're going to measure distance between nasal sound on a nasal sound here.
Now, maybe it's the case that nasal like, extremely predictable, that have very tight distribution.
They don't very, very much.
They're very, very similar to each other.
Well, let's imagine that Worst sounds extremely variable.
They're all over the place.
So what looks like a big distance from the work to our work might not really be very big.
It might just be within the range of normal variation of what sounds, Whereas if we have the same sort of distance we know, we know that normally these things are very tightly distributed.
We know these things are very dissimilar, so there's some natural variance within these different classes and is different for each class.
That's what I'm going to try and account for with probabilities.
We're not going to try and guess we're not going to say from our acoustic genetic knowledge that was more variable and knows the less variable, which is going to learn it from data.
We're going to look at data and say How much do things very within a class, we're going to use that to normalise our distance measures.
To get an idea of what counts is a big distance, and what counts is a small distance.
So let's start with this example.
So what do we got here? We're just doing the local distance between one vector on another factor.
What I've got is a collection of vectors of one particular class.
So these green things air of one particular class on the blue things over.
Another particular class I'm going to now have unknown.
So these are collections of reference vectors sees these references of green, and these are references of blue going too.
Come along now and do pass and recognition just for a single frame.
I'm gonna put my unknown vector into this diagram and say, Is it the green thing or a blue thing? So let's just put it somewhere.
Let's put it here.
Okay, let's use the Euclidean distance to decide.
Is it blue or is it green? So the distance to the average blue thing is this much.
The distance to the average green thing is this much.
We're going to announce the answer as being blue.
Okay, because it's nearer the middle of the blue things now, looking at these clouds of green things in clouds of blue things, what do you think the answer is? You think it's green or blue? It's clearly green because the green things are distributed all over here on the blue.
Things only distributed around here, and this is clearly within the scope of the green things.
So how are we going to find the distance measure that would correctly classify this unknown point of belonging to the green distribution and not the blue distribution? And the answer is, I got to take account of this variance.
How far away from the average from the mean Do we normally expect things of this type to go? We're going to normalise the distance by that.
Rather, just the absolute distance to the average is going to be the absolute distance, normalised by how much we would normally expect things to vary from the average going normalised Euclidean distance.
We're going to derive that properly in the news probabilities to represent it.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
we're going to now switch to thinking not off samples of things.
So here, samples of things with the template is an actual recording of a one.
The unknown is an actual recording of something that may or may not be a one.
We're measuring distance between samples.
There's no model.
We actually stored data.
When we come to do pattern recognition, we have that store data ready to go.
We're going to get rid of the data and instead fit a statistical model to it and just keep a statistical model.
We're going to steal everything we need to know about the data into a model and then throw the data away.
So just be training data for estimating the model.
So how might we store model? What might a model of something looked like? Well, so far, it's very naive.
It's just the actual examples that's not very efficient.
It's going to very large thing to store.
It's very hard to do computation with, so we might then start distilling that information down into just the things we need to know to make classification decisions.
So instead of storing actual points, well might, for example, been them into values and store their history, Ma'am, my fitter paramedic function to their distribution.
And that might be something like a galaxy.
This is, in fact, what we're going to do now.
It could affect the distribution, so we're going to use this galaxy and distribution on the gas and distribution is the mother of all probability distributions.
It has the nicest mathematical properties.
It's the most simple to do computation with.
It's got a very small number of parameters.
There's only two numbers we need to represent the calcium, and that's the average.
That's this middle point.
Here we call that mu.
That's the Greek letter Myu.
It's just me because you start with me.
Nothing fancier than that on DH.
The spread around the mean And then that's gonna be the standard deviation.
We're going to call that Sigma Sigma starts with us.
Esther Standard Deviation.
There's nothing clever about Greek letters were just trying to look fancy by using them.
Mr The Standard notation we're gonna still mean on the standard deviation we might equivalently.
Instead of scoring signal, we might store Sigma squared, and that's called the variance variances done.
Deviation.
One is just a square of the other.
There's just two numbers that describe that curve.
That looks good because we don't have to start to numbers instead of a whole cloud of data points.
So how might we fit the probability density function to some data on What is it going to help us with? So that's the equation for the calcium.
I don't know if you don't stand that, but I do encourage you to go away and think about how this equation works.
Put some values in it and see what numbers you get out, for example, So this is the parameter of interest.
That might be the energy in one of the bins off.
Pfft.
It might be the fourth element of our feature.
Vector is going to give it a number.
It's a variable called X.
I mean is the average mu.
When X equals Myu, this term goes to zero.
When this time goes to zero, this whole thing has a maximum value, and that's we're here.
So for data points that are near the average of the distribution, the probability is the highest.
That's intuitively reasonable.
So things near the centre of distribution of a high probability on the further away.
We go from the mean in this direction or this direction.
The lower the probability girls now technically, this is called a probability density.
It's not actually probability, but for the purposes of this course, weaken gloss over this subtle difference.
For now, just think of it as probability.
Or how likely is it that the Value X belongs to this distribution? We can see that sigma occurs in the sigma squared form here, which is often why we store Sigma squared calling variants equivalent Weaken Store Sigma recalled its standard deviation.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
So this form of this equation, this equation here, generalises to any number of dimensions and it's got two parameters.
It's got an average, I mean and it's got a deviation around that average.
Let's see what happens to those parameters as goto higher numbers of dimensions.
Let's draw this very, very simple One in two dimensions average here, I mean, and this is two dimensional.
So the mean is a vector with two numbers.
I mean, a long one dimension mean along the other dimension on this distribution here is just uniform.
It's circular and in high dimensions would say it was a miracle.
In other words, the distance in all directions is the same.
So that means we could just store one number for that Sigma sigma.
We could just all one number two, standard deviation, every direction, the deviations, the same.
So there are three parameters to this uniformly distributed circular calcium threes and my small number.
What about this distribution here? So the underlying data is now no longer evenly distributed.
All the different dimensions, the desert.
The variance in this dimension is smaller than the variance in this dimension.
So what we need to store now still need to store the mean on the mean is a vector of two numbers.
We now need to store the variance in both directions.
So Sigma is also going to be a vector of two numbers variants one way and variance the other way up with that.
So this distribution little more complicated than the previous one.
We now need to store four numbers to represent it, not three numbers.
It's got more complicated.
Still, how about the data that distributed like this? There's now some correlation between the two values data points that have a high value in this dimension.
On average, 10 toe also have a high value in this other dimension to the correlated, not independent anymore in the statistical sense.
So now we need to still stole the mean.
That means still a factor of two dimensions.
We also need to store the variance in these two directions.
It might be different, so the variance looks like it might be two dimensional, but we also need to store some additional things.
And that's these co variances.
How much does Co very.
In other words, what slope of this house cute is this against the axis, so the various actually good to become a matrix of four numbers I should be a symmetrical matrix only has three independent values, so you got even more numbers to store.
This case is a particularly nasty case because this variance here, let's change this number because in general, when becomes a matrix, we change the letter.
It's a big segment out to imply that Big Matrix this has got a lot more parameters than the previous one.
And imagine what happens when we go above two dimensions.
We got three dimensions for dimensions, 39 dimensions.
This matrix is going to get bigger and bigger.
There's the three dimensional version.
It's got nine things in it.
So the number of parameters in the variants goes up like the square of the dimensions.
So you can imagine a model that's operating in high dimensional space, maybe ar 15 magnitude spectrum with 1000 points in it.
This matrix is 1000 by 1000.
There's a very large number of the order of a million parameters in matrix.
That's a very bad thing, because to estimate the parameters, we need data points and more parameters that are, let's just stick with this intuitively, the more parameters that are more data points, we're going to need to estimate the parameters reliably.
So distributions looked like this where the correlation between different dimensions really bad news because our probability distribution will have a lot more parameters to estimate.
That means we need a lot more data to estimate the parameters and the number of parameters goes up like the square of the dimension.
That's a very bad thing goes up like best with dimensions.
So we're going to try and avoid this situation.
All costs in statistics.
We call it a correlation when one value tends to vary with another value, this is positive correlation.
Everything was twisted the other way.
They might be negative correlation.
We're going to use the probability term, which is essentially the same thing.
That's co VarianMS they co very.
When one varies, the other tensed area with it in sympathy go up and down together, we'll be going up directions together.
The highly correlated

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
So here's a county in, okay, Just just like that one between two dimensions on this is the probability of these two dimensions.
Probably density.
Okay, now is not convenient to draw these fancy three D diagrams as colourful as they look.
So we're just going to do a bird's eye view is going to look down on it like it was a map and hopefully you can all read maps.
To some extent, we're going to just draw the contour lines.
Okay.
Remember one way of representing three D things like the landscape is above, which is contour lines of equal height.
I was going to draw them with control lines and I was gonna go one contour line.
So here we are now looking down on top of these two dimensional galaxy ins.
On this distance, here is the standard deviation.
So that's the standard deviation green things.
And that's standard deviation of blue things.
Now what we can do, we're going to classify this unknown point.
We're going to do it this way.
Here's the thing we're trying to classify.
It was about here.
We're now going to work the point we're trying to classify, we decide Is it more like it? That's green or blue.
We're gonna work out the probability of it being green, so we know it's got a feature vector.
There's it's two dimensional feature vector.
We just plug that feature factor into the formula for calcium.
So here's the formula for gasoline and thatjust generalises to any number of dimensions, and we get a probability value.
That's the probability of it being green when we get to probability of it being blue and we just compare those two numbers.
And in this particular case, the probability of being green is going to be higher than the probability of being blue.
So we're going to classify that as a green thing.
Let's do it like a simpler version of it in one dimension just to make that really clear.
So let's just let's just imagine we're just doing things in this dimension.
You can draw along the top, so the galaxy in of the blue things looks like this is quite narrow on the gas and the green things.
Let's do things in the correct colours.
Let's just let's just take this ex dimension to it, back it back in one dimension.
Let's do the density function of blue things.
This is quite peaky.
Distribution, like that.
Distribution of green things has the means here, and it looks something like this much wider.
Now we want to classify some unknown value of X.
So along comes a value X.
Is it more like to be green or blue? So maybe the value is here.
That's X one, and we just go and see which of the curves is higher on the high school.
Blues is a blue thing.
Maybe there's an X here next to his ex green or blue.
The highest curve is a green thing.
We can see there were these two cross.
There's just an implicit boundary between the two classes, so these two probability distributions form a very simple form of classifier in the classified just has a boundary and effectively all this classifier says.
If X is less than this value, it's blue.
It's more than this value.
It's green.
That boundary is implied by these two probability distributions, and the same is true in two dimensions.
So some implied class boundary here.
Between these two things, it's not going to be exactly straight into something like this.
on this boundaries implied by these two distributions.
We never draw this boundary.
We never need to write it down or we need to do is for any point in space.
We just compute the probability of it being green, probably being blue.
Compare the two numbers in whichever's highest is what we classify this point us.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
Now, before we go on, let's just not derive but simply state and its into it enough to state it.
How do we estimate the mean on the variance of the calcium? Let's go back to some.
This one here.
So imagine we've got some data points.
We've got those data points and they all belong to the same class.
There are green things or blue things or or they're all words on Nurse.
How do we estimate Mu and Sigma? Well, there's these parameters here, Mu and Sigma.
We're just going to state without proof, because so obvious.
I think you're just going to accept it in the best possible estimate from you.
They're just the average value of the data points.
The best estimate of the mean of the calcium is the mean of the data about the empirical means.
Unsurprisingly, the best estimate of the standard deviation is the standard deviation of the data about that data point we could derive from first principles.
We're not going to beyond our scope and in fact, those estimates those estimates of taking the average of the data and taking the standard deviation of the data.
These empirical estimates of meaning VarianMS very important there, Well motivated.
And they're the ones that make the training data as likely as possible toe have been generated from this particular problem to distribution, So the estimates are what we call maximum likelihood estimates.
There are other ways of estimating the prime minister probably distributions, but this is the simplest and the most obvious, and the one we're going to use the maximum likelihood estimates.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
I'll just point out one little technical detail that turns out to be not important, but we need to state it.
Just to be truthful, this value on this axis is not actual probability.
That's what's called probability density probabilities.
We're going right with a big piece.
Usually, if we're being strict, we're going to be that sloppy on the slides coming up big piece of true probabilities and some upto one.
So, for example, I got this coin I toss this coin on, decide with heads or tails some of the probability of it being a head, plus the probability of it being a tail equals one because it's one or the other.
How many times I do it? Add them all up.
Always add up to one, because X here is a continuous value, not discreet heads and tails is a discreet thing because there's a continuous value could actually take an infinite number of possible values along the scale.
Okay, so it's a scaled, continuous value, and what that means is that we can't make these probably density some 21 What sums to one is the area under this thing? Not that just not the sum of the heights.
Okay, So into the integral, integral integration, the area sums to one.
It's not important because it's just proportional to problems.
So we're going to use the word probability a little bit.
Sloppily, we might mean density, but for this course, that's not an important distinction.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
I'm going to look at the side of conditional probability, huh? And that is that knowing one thing now is informative about some other things.
There's some conditional dependency between correlated and specifically in this example.
Knowing which age men were using does change the probability of the observation sequence.
That's kind of the point.
Okay, well, then developed into a very simple probability real called basil, which is critical.
If we're going to use that to do all of the work of speech recognition, will name the items in that in that rule.
And then we're going to look at how we do recognition with a chairman's on which terms in this bays rule in this equation.
Hmm computes And then we realise, is another term that the ancients don't compute and we go to another model to do that, that's going to be called a language model.
So conditional.
Independence, independence.
So if things are independent, everything's great.
Just compute everything separately and just product.
Multiply them together.
That's all fine.
Okay, what if things are not independent? So let's think about two things, depending on each other, the height of the people in this room we could draw distribution of that.
Or we could say that Somebody waiting outside there and we're gonna guess their height before they come in and play a guessing game.
How accurately we gonna guess their height? Well, if we don't know anything about them, we're just going to guess the mean of all the people in this room, Here's our training data.
Maybe.
I mean, high 1.7 metres.
So whoever comes in the room guest 1.7 metres.
Not with the minimum era.
Gas on average, will be closest with guests.
And then now let's play another game.
I'm going to tell you something about the person is about to come in the room.
I'm going to say it's a man.
Maybe, I guess is now going to be.
We're gonna get there 1.8 metres.
It's a woman.
We're gonna get there maybe 1.6 metres.
So knowing something about them is informative about the other thing.
These things are not conditioned independent.
Knowing somebody's gender, no male female will help you guess their height on average for individual cases, not always.
We're going to find short men and tall women.
But on average, we're going to do better if we know one thing.
Gonna help us.
Guess the other thing.
So we got this notation for this.
We've just seen it on.
The same thing applies to Hidden Markov model.
It turns out then, that are hidden Markov model.
Compute the probability of an observation sequence, given the identity of the model.
Given which model is it? A model of one among to on the 31 of nine.
We're going to use a notation for that w big capital.
W means it's the random variable for word.
It could take one or two or three and knowing so we could compute things like probability that the observation sequence equals the particular one that we've been given that we try to recognise.
Given that the word equals two so we can compete things like that with hidden Markov models

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
that's what a remarkable can compute for us.
Unfortunately, that's not really what we want.
We're not really interested in the probability of some speech.
We want the probability of particular word sequence, given that we've Bean given this speech and turned into a sequence of embassy sees given that speech.
So that's after this.
Bart could be given speech.
Tell me, how likely is it was a one.
How likely is it too? How likely is it is a three.
Compute all of those and pick the biggest one.
So really, What? We want to compute this thing here.
Probability of a word.
Be a particular word.
Given the speech, Bob just means given.
But the hit a market model does not compute that we could think of other models that might directly compute that some discriminative models fancy thing.
But our hmm does not complete at the Richmond is a generative model, and it generates speech.
Therefore, compute the probability of that speech, not the probability of the word.
So it computes this thing here, so we're gonna have to get one of these things from the other thing that we could do that fairly straightforwardly.
There's a very simple law of probability.
I'm going to state it and just tell you it's true.
We're just look intuitively about why this is reasonable.
The joint probability of two things where one of them is informative about the other is equal to this is equal to the probability of one of the things.
So let's look at one of them and then given that thing now we know its value.
What's the conditional probability? The other one? So it's equal to the probability of one of the things it doesn't matter which one multiplied by the probability of the other thing.
Given that we now know that the value now if these two things were independent, that will just reduced to probability of oh, probability of W because probably oh, given W.
Would be just probably oh, if they were completely independent.
Knowing W wouldn't change.
Probably developed, we just reduced about.
However, that's not the case.
If they are co variant, they depend on each other.
One is a war motive about the other, so we can write that equation down hope that's just intuitive, reasonable and CNN's own w we just letters.
We could write ABC any letters we want.
So we just swapo on w just notation so we could buy symmetry.
Just write this other thing down.
Okay? Now, probability off.
Oh, on w is exactly equal to the probability of w on DH.
Okay, Word on DH, just what things around.
Okay, probability of someone being this and this is that it is equal to the probability of being two things just said in the other way, it doesn't change that probability.
So because of that, these two things exactly equal to each other and therefore this thing is exactly equal to this thing.
We rearrange that, then get this lovely equation down here on.
This is so important.
It's got a name.
It's called Bays Rule and magically tells us to how to compute what we need to compute in terms of the thing.
The hmm can compute on some other terms.
That one we know.
We're there with that one.
We'll see in a minute exactly how to compute it.
R h man will do that.
Where on earth were gonna get P f w and P r go on their own from? We'll deal with those things.
So there's the full thing spelled out.
Let's give this thing some special names.
This thing here is a conditional probability.
So hmm, actually compute the conditional probability Probability often Observation sequence.
In other words, a sequence of M sec vectors.
Okay, this's oh, it compute the probability that, given that you give me a model to compute the probability the models got a label on the label is this w So is this conditional probability that's gonna be okay?

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
What about these other terms here? This P W there's no Oh there.
So it doesn't matter if I've given you the observations are not yet weaken.
Compute PW separately without ever seeing.
In other words, we could do even before we start doing speech recognition.
Before we even record the speech or anything, we could compute this p o.
W term because we could do it in advance.
It's called a prior.
That means we know it before we even start doing any of this computation.
And it's just a probability off the word or the word sequence.
More generally, for example, in a digit, recognise her if all of our words equally likely going to have a pee of W equals one that's good equal, attend w equals two people want 10.
So maybe that's just simply uniform distribution.
But for a more interesting task, it might be Some words are more likely than other ones.
It might not be in uniform distribution.
We could see that we could compute that ahead of time.
We don't need any speech for that.
You get ahead of time.
We look at how we do that later, so that's got a bit of an idea about how we might be able to get that it's something to do with the probabilities of words or sequences of words, including collected speech.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
So that's our hmm that we can have a guess about how we're gonna computer and we'll probably later.
This thing on the bottom's a bit weird.
It's just the probability of the speech was just being given.
Now how would we compute the probability of just some secrets of our CC vectors? Well, the only way we could do that it's just to see all possible sequences, ever CT vectors, and then look this one up in that distribution and say This is a really likely sequence of the mercy seat.
There's really unlikely sequence of species that would be a really, really hard thing to compute content out.
We don't need a computer.
That's okay, and we'll say precisely why Just in a minute, Okay, this is a thing that we want, and it's the thing that we want to use for the classification task.
So we were trying to maximise the value of this by varying W to make this term's biggest possible and then announced that W as the winner because this's found after getting the observations.
It's called the posterior austerity just means after this post here is a popular for this.
Okay, so the terms on the right inside.
Then Pierrot given W.
Is the likelihood that a German computes it.
W is the fryer is going to computed by something called the language model MP.
Evo is the prior on the observations.
It's a bit of a weird thing.
Think about what happens when we run the speech.
Recognise er, we get given a no fixed oh secrets of Assisi vectors.
Go look at them in the files with H List.
Print them out for the purpose of that one run of the recognise er between receiving it on printing the worst sequence out.
That's a constant.
Let's give him it doesn't really matter what probabilities maybe is probably his 0.3 May's probably ability is 0.1.
It never changes.
It's a constant, so it means we don't need a computer.
So this thing here is some unknown constant value.
We don't know what it is, but it's constant.
It's fixed, so just imagine it taking some value, I don't know, no idea what he was going to take.
So during recognition, we're just going to very w going to sweep through the recovery of W's trying to maximise this term here Gonna try this? W try this other dude.
You try the others, we're going to search amongst all the values that W could take for the W that makes this term's biggest possible.
And as we sweeping the W, it's just isolated words.
We just try one each in turn that sequence of words with final the sequences as we're doing that Oh, never changes.
So this value on the right never changes.
So we could just turn this equal sign into this other sign.
This just means proportional to, you know, there was a equals, a constant times, this thing just a scaled version of it.
And the constant is Pierrot.
So what really going to do is this thing Pierre was gone.
Good news, because it turns out to be really, really hard to calculate some sorts of models out there.
Fancy descriptive models need to compute turns like that's a big problem.
Arrangements.
We do not need to compute it.
So we don't have the thing.
The hmm computes thing.
This language model that's gonna come later computes we're ready to go.
We're just going to now compute each of those two terms They were going to very w across all the different values W could take for one of those values.
This value here will be the biggest, the maximum, and that's the W will announces the recognition results.
Okay, happy.
So decide.
They're sweeping across all of our use of W the space of all possible W's in our isolated.
Did you recognise her? Is very small and finite.
It's just 10 possible values we just couldn't list.
Try them in turn.
But more generally, it might be a sequence of words, and so we have to search amongst all possible sequences, so there might be some clever things we need to do there.
We'll come on to that later.

This video just has a plain transcript, not time-aligned to the videoTHIS IS AN UNCORRECTED AUTOMATIC TRANSCRIPT. IT MAY BE CORRECTED LATER IF TIME PERMITS
so don't use a prior it's a language model will look at how do that in a minute.
The posterior is the thing we're after.
It's just the product off this likelihood on this prior.
So let's just think about that in these bays in terms before we even start the speech recognition we have in our mind a mental model of P.
O W.
You've all appear w in your minds.
Now you are making predictions about the next word.
I'm going to say you're making good predictions.
You're finding it easy to understand me if I just suddenly unexpectedly banana, say a word that you would expect You're not going to find that as easy to process.
Okay, so your language model did not have that he was there, but with a very, very low probability that then became harder for you to process.
So we're sitting there waiting with belief about what W will be with Beijing.
It's Noah value the distribution, but it's a non uniform distribution.
Something's likely something less like we're sitting there waiting with some belief.
Along comes some evidence in the form of a speech signal on the speech signal.
Revise is those beliefs, our beliefs after we hear what I've said different before, what I've said, hopefully unless I'm totally predictable.
Okay, which case my signals, totally uninformative.
Prior just takes over.
Hopefully there is some information in the speak stream and that revise your beliefs about BMW.
Thanks.
So this posterior is the prior POW, but revised now that we've seen.
So it's a distribution overall, lots of worse sequences, but it's being revised and it might be revised to the point where we're absolutely certain it was this word and we totally said it was none of the other words or it might be just a bit more spiky, hopefully got lesson for me.